
Analysis of the Principle of Spherical Reflector
The law of reflection can be regarded as a special case of the law of refraction when n=-n’. Therefore, in the formula for the refractive sphere, as long as n=-n’, the corresponding formula for the reflective sphere can be directly derived. 1. The object-image position formula of a spherical reflector
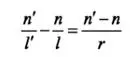
The above formula shows the relationship between the object image position l and l’ of the refractive sphere. Substituting n = -n’ into the above formula, the object image position formula of the spherical reflector can be obtained:
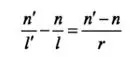
A single refractive spherical surface cannot be used as a basic imaging element (a reflector is a special case of a refractive surface and can be a basic imaging element composed of a single surface). A basic imaging element is a lens composed of at least two spherical or aspherical surfaces. For ease of processing, most lenses are composed of spherical surfaces. The object-image relationship of a spherical reflector is shown in Figure 1. Figure 1(a) is a concave mirror, and Figure 1(b) is a convex mirror imaging an object at a finite distance.
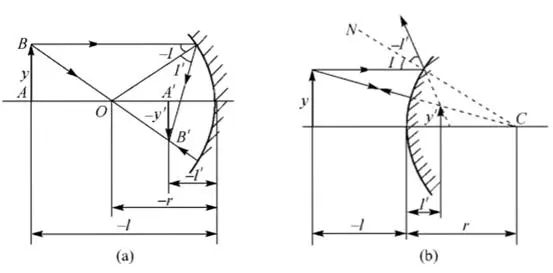
Figure 1: Object-image relationship of spherical reflector 2. Imaging magnification of spherical reflector Substituting n=-n’ into the three magnification formulas, the three magnification formulas of spherical reflector are obtained as follows:
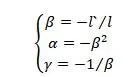
From the above formula, we can know that the axial magnification α of the spherical reflector is a negative value. When the object moves along the optical axis, the image always moves along the axis in the opposite direction. However, when the reflection is an even number of times, the axial magnification is positive. When the object is at the center of the spherical reflector, l=l’=r, and the magnification at the center is
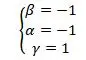
From the reflection theorem, we know that: I’=-I, that is, the angle between the reflected light and the incident light is π-2I. When the object point is located at the center of the spherical reflector, the triangular optical path calculation formula shows that I’=I=0, and the angle between the reflected light and the incident light is π, that is, the light passing through the center of the sphere is reflected back by the reflector along the original path, or in other words, any light emitted from the object point at the center of curvature of the spherical reflector will still converge at this point after reflection, and the spherical reflector is an equal optical path surface for its center of curvature. 3. Lach’s invariant of the spherical reflector Substituting n=-n’ into the Lach’s invariant of the spherical reflector:
Hanzhong Brisun Optics Co., Ltd. Is the high precision optical element manufacturer provides customized production of Various optical lenses, including spherical lens, cylindrical lens, optical window, mirror, prism, filter, metal base mirror and other high-precision optical elements. The base materials include various optical glass, fused quartz, calcium fluoride (CaF2), zinc selenide (ZnSe), germanium (GE), silicon (SI), sapphire, metal and other materials. And provide antireflective film, high reflection film, spectroscopic film, metal film and other optical coatings.
Welcome to OEM and Purchasing!


