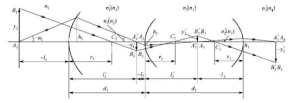
I believe that students have encountered such problems as “whether reading glasses are convex lens or concave lens” when doing questions. Convex lens is the lens knowledge of our junior middle school physics study. From this chapter, we know some laws of lens imaging. What can we do through these laws? In other words, what are the applications of convex lens in our life?
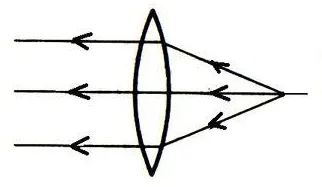
1. Function of convex lens
The function of convex lens is the convergence line and imaging. Convex lens can form both real image and virtual image, and can form both enlarged image and reduced image.
1.1 convergence
Let a beam of light parallel to the main optical axis shine on the convex lens, and it is observed that the refracted light is a convergent beam, that is, the convex lens has a convergence effect on the light. A point where light rays converge and intersect one side of the convex lens. This point is called the “focus” of the convex lens, which is represented by “F”; The focus of the convex lens is the real focus, one on each side, and there are two real focus in total; The distance from the focal point to the optical center O is called the “focal length” of the convex lens, which is represented by “F”.
Convergence refers to the effect of convex lens on light. The refracted light passing through the convex lens converges or diverges less than the incident light, as shown in Figure a. Convex lens can converge not only parallel beams, but also divergent beams. “Convergence” does not mean that the refracted light passing through the convex lens is a convergent beam.
1.2 imaging function
The imaging law of convex lens is an optical law. In optics, the image formed by the convergence of actual light and can be presented on the light screen is called real image; The image formed by the convergence of the reverse extension line of light and cannot be presented on the light screen is called virtual image. When talking about the difference between real images and virtual images, we often mention such a distinction method: “real images are inverted, while virtual images are upright.” If it is a thick meniscus concave lens, the situation will be more complicated. When the thickness is large enough, it is equivalent to Galileo telescope, and when the thickness is larger, it will be equivalent to positive lens.
End